Menghitung Operasi Matriks dengan Menggunakan Microsoft Excel

Matriks adalah susunan bilangan yang berbentuk persegi panjang yang diatur menurut baris dan kolom serta diapit oleh sepasang kolom siku (lho..lho..lho... koq malah ngebahas definisinya sich), ya aggep ja sbg pembuka gitu, he... OK lah klo begitu !!!

Dalam matriks terdapat beberapa operasi yg berlaku antara lain adl : penjumlahan, pengurangan, perkalian, transpose, determinant dan invers. Nah bagaimanakah cara untuk menghitungnya ???. Klo cuman matriks yg ordonya dikit sih tinggal itung manual ja tapi klo ordo nya banyak (misal : inverse dari matriks berodro 8 x 8) ya bisa botak tu kepala tuk ngitungnya, tapi da caranya koq pakai ja ”MATLAB” bwat ngitungnya, tinggal install di komputer lalu klo mo ngitung matriks tinggal masukin matriksnya lalu Enter maka muncul deh hasilnya.

Tapi Q baru tau beberapa waktu yg lalu klo ternyata eh ternyata Excel juga bisa lho ngitung operasi2 matriks diatas. Nah bagi yg belom tau ni Q kan nulis mengenai itu, ya... itung2 kan bisa mempermudah bwat ngitung operasi2 matriks yg ukurannya besar tanpa harus nginstall matlab di komputer kmu.

Dalam excel, matriks ditulis dengan cara memasukkan elemen2 matriks ke dalam kotak / sel (pada excel) yg bersesuaian. Misalkan qta mo nulis matriks dibawah ini :

                     1       3       1

                     2       1       4

                     2       5       2

Maka penulisan di dalam excel adl sbb (dimisalkan qta tulis dalam sel A1 ampe C3, jadi matriks dapat ditempatkan di sel mana saja asal penulisan bersesuaian dengan elemen2 matriks) :

Nah untuk ngitung operasi matriksnya berikut ini Q bahas satu per satu.

1.      Transpose Matriks

                                                      1       3       1

Contoh : Transpose dari                2       1       4

                                                      2       5       2

Langkah2 nya sbb :

>       Tulis matriks ke dalam excel spt cara di atas !

>  Ambil range mana yg akan dipakai untuk menempatkan hasil transpose, misalkan range dari sel A5 ampe C7 (range A5:C7), maka blok range tersebut !

>  Ketiklah rumus berikut ! ” = TRANSPOSE(A1:C3) ” . Pada rumus A1:C3 selain dpt ditulis langsung bisa juga diperoleh dengan mengeblok range A1:C3 shg rumus akan otomatis tertulis.

>       Tekan kombinasi tombol Ctrl + Shift + Enter, maka hasil transpose akan terlihat di range A5:C7.

2.      Determinan Matriks

                                                      1       3       1

Contoh : Transpose dari                2       1       4

                                                      2       5       2

Langkah2 nya sbb :

>       Tulis matriks ke dalam excel!

>  Ambil sel mana yg akan dipakai untuk menempatkan hasil Determinan, misalkan A5, maka blok sel tersebut (ingat, qta mengambil sel krn hasil determinan berupa nilai bukan matriks)!

>      Ketiklah rumus berikut ! ” = MDETERM(A1:C3) ”. Ato pakai cara pengeblokkan.

>      Tekan kombinasi tombol Ctrl + Shift + Enter, maka hasil determinan akan terlihat di sel A5.

3.      Inverse Matriks

Dalam mencari invers harus didasarkan pada aturan matriks yaitu matriks akan punya invers jika determinan tidak 0, jika determinan = 0, maka matriks tidak punya invers dan jika tetap dicari maka hasil di excel akan bertuliskan #NUM.

                                             1       3       1

Contoh : Invers dari              2       1       4

                                             2       5       2

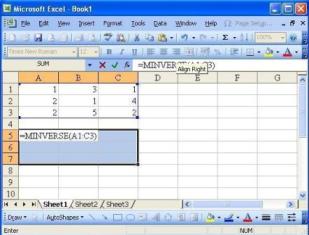
Langkah2 nya sbb :

>       Tulis matriks ke dalam excel!

>  Ambil range mana yg akan dipakai untuk menempatkan hasil transpose, misalkan range dari sel A5 ampe C7 (range A5:C7), maka blok range tersebut !

>       Ketiklah rumus berikut ! ” = MINVERSE(A1:C3) ” . Ato pakai cara pengeblokkan.

>       Tekan kombinasi tombol Ctrl + Shift + Enter, maka hasil inverse akan terlihat di range A5:C7.

4.      Penjumlahan dan Pengurangan  Matriks

Dalam penjumlahan dan pegurangan matriks harus mengacu pada syaratnya yaitu 2 matriks yg ditambah ato dikurangi harus berukuran/berordo sama

                        1       3       1                3       6       5

Contoh :           2       1       4       +       1       7       2

                        2       5       2                9       4       8

Langkah2 nya sbb :

>      Tulis matriks ke dalam excel (misal matriks pertama ditulis di A1:C3 dan matriks kedua ditulis di A5:C7)!

>       Ambil range mana yg akan di pakai untuk menempatkan hasil penjumlahan, misalkan range E3: G5, maka blok range tersebut !

>       Ketiklah rumus berikut ! ” = A1:C3+A5:C7 ” . Ato pakai cara pengeblokkan.

>       Tekan kombinasi tombol Ctrl + Shift + Enter, maka hasil penjumlahan akan terlihat di range E3:G5.

Untuk pengurangan caranya sama dengan penjumlahan yaitu dengan mengubah tanda ’+’ dangan ’-’ .\

5.      Perkalian Matriks

Dalam perkalian matriks harus mengacu pada syaratnya yaitu 2 matriks dapat dikalikan satu sama lain jika jumlah kolom matriks pertama sama dengan jumlah baris matriks kedua, jadi matriks A yg berordo p x q dapat dikalikan dengan matriks B yg berordo  r x s jika q = r dan hasilnya adalah matriks baru yg berordo p x s.

                        1       3       1                3       6       5

Contoh :           2       1       4       x       1       7       2

                        2       5       2                9       4       8

Langkah2 nya sbb :

>      Tulis matriks ke dalam excel (misal matriks pertama ditulis di A1:C3 dan matriks kedua ditulis di A5:C7)!

>       Ambil range mana yg akan di pakai untuk menempatkan hasil perkalian, misalkan range E3: G5, maka blok range tersebut !

>   Ketiklah rumus berikut ! ” = MMULT(A1:C3;A5:C7) ” . Ato pakai cara pengeblokkan.

>       Tekan kombinasi tombol Ctrl + Shift + Enter, maka hasil perkalian akan terlihat di range E3:G5.

Nah demikianlah cara2 perhitungan operasi2 dalam matriks memakai Ms. Excel. Tentu saja matriks yg dapat dihitung bukan hanya yg berodro kecil tetapi juga yg berordo besar. Jadi bisa    2 x 2, 3 x 3, 4 x 4, 5 x 5, 6 x 6, 7 x 7, 8 x 8, dst.